前言

经常在各种方法的推导中见到拉格朗日乘子法，不懂的时候是一见一个怵。这里就对其进行一个解的理，以便看懂以及自己也用上

看到一个写拉格朗日乘子法和KKT条件的博客不错。可以点击这里查看

拉格朗日乘子法

拉格朗日乘子法（Lagrange multipliers）其实也就是一种寻找多元函数在一组约束下的极值的方法。是一种比较直观且简单的方法。公式如下：

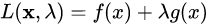
其中f(x)是被求极值的函数，g(x)是约束条件，λ就是拉格朗日算子，是一个常数。实际工作的时候要求极值，就直接对该函数求导

通过引入拉格朗日乘子，可将有d个变量与k个约束条件的最优化问题转化为具有d+k个变量的无约束优化问题求解。也就是把各种变量和约束条件以一个更方便的方式组合到一起求解。

可能第一次见这句话还会有些看不懂，不知道他是怎么做到这一步的。我们下面来对其进行解释。

等式约束下的拉格朗日乘子法

下面抛出一个问题：
我们要求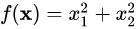的最小值，条件是在约束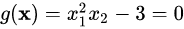下。

我们来尝试解决这个问题。
一般最朴素直观的解决方法就是将g(x)中x1,x2代入到f(x)里进行一个参数的替换。给替换参数后的f(x)求极值可解。
解法如下：

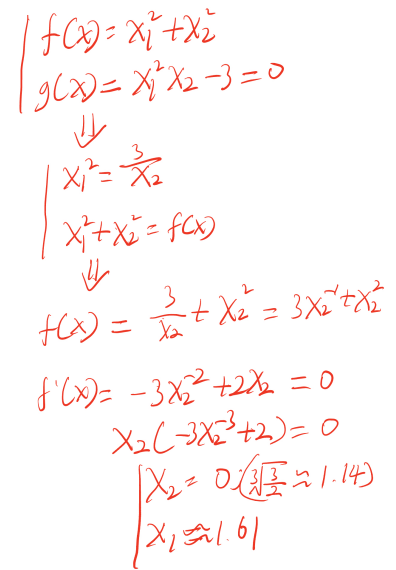
后证明X2不能为0.（字不好看轻喷。。）

对于只有两三种未知数的式子这种朴素的解法其实也还好解,但是如果我们的未知数一旦多了，复杂度则是指数型上升。。而且这种算法本身也不是特别的便利

那若使用可以应对更多未知数和约束条件的拉格朗日乘子法，这个问题要怎么解决呢？
我们首先知道，在一个等式约束中，函数的极值一定是在函数与约束的切线上的。有以上的任务画图如下

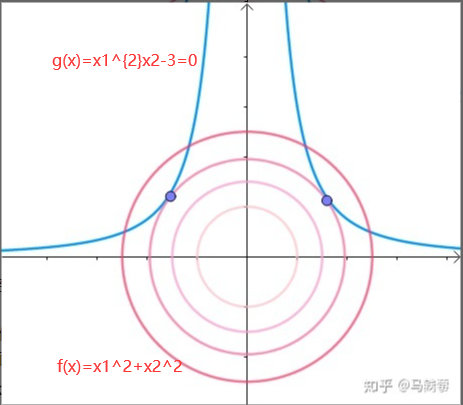
蓝色的结点就是二者交点。在交点上我们有f(x)的导数梯度与g(x)的导数梯度方向一定相同或相反。也就是说，若满足那就是在交点上，也就是取了极值了（λ是变量，是常数）

而同时我们又有约束条件g(x)=0，所以也就得到了以下的式子

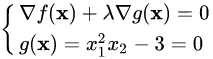
实际上，以上的式子做一点泛化就是在等式约束下的拉格朗日算子法了。泛化结果如下：

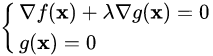
而我们正巧又发现，二式的最简单的原函数就是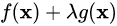，也就是我们对拉格朗日算子法的公式定义。上面展开的式子分别就是对这个式子对x和λ的偏导。

我们代入上述问题到式子中，则有解

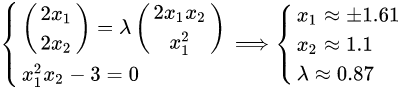
与上面我们手算的结果一致！而我们做的计算量则因为对变量的求导大大减少了。
只需要一个L(x) = f(x)+λg(x)
这也应了前面我们对拉格朗日乘子法的定义，就是将有d个变量与k个约束条件的最优化问题转化为具有d+k个变量的无约束优化问题求解。

在不等式约束的情况下？

因为约束是不等式，所以与等式约束的最大区别就是，等式约束要求值在一条线上，不等式约束要求值在一个区域里。【但是若极值点在等式约束范围之外，还是切点上取极值】

既然是一个区域的约束，那当对一个函数求极值的约束是不等式时，则需要分情况讨论了。

一种是，极值点在不等式约束之内，则不需要不等式约束也可以找到极值点且不需要在切线上找。【λ=0{不需要g(x)}，g(x)!=0{取极值点时}】
第二种是，极值点在不等式约束之外，取不到极值点。则需要再在边界上找极值点，那就等于等式约束了。【λ!=0{需要g(x)},g(x)=0{在边界上取极值}】

那么这两种情况同时满足时，就是λg(x)=0。有如下式子

这也就是KKT条件。

有不等式有等式约束的混合情况？

若碰到这种情况

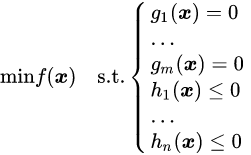
其中g(x)是等式约束的集合，h(x)是不等式约束的集合。无论有多少个

我们则有拉格朗日定义如下：

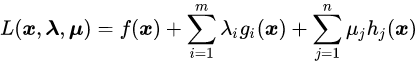
也就是约束条件如下：

这个式子也就是KKT条件 （最优化条件，由Karush[1939]，以及Kuhn和Tucker[1951]这三个发表所以叫KKT）。
满足这KKT条件的不一定是是局部(全局)最优点，可能是极大点或者是鞍点。但是局部(全局)最优解一定满足KKT条件。而且在KKT条件里面的一定有全局最优解。
若待优化函数是个凸函数，满足KKT条件也就一定是全局最优解.【学习凸函数优化的重要性。。】

最后一个混合情况的例题给出，请大家算算吧

Q.E.D.