对于一些散度之前不是很熟，而对这种重要评价标准看不懂会让人很难受哇。。所以今天正好补全了，最近开始比较常写博客了

KL散度

要理解KL散度,就先来介绍一下信息论中一个基本的概念"熵"

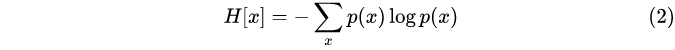
熵是一个什么样的概念呢？是发送者想发送一个随机变量p(x)给接受者时，需要传输的平均信息量，也就是某个随机变量在概率下的加权平均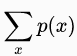（ = 1）。

也就是说熵是一个比较全局性的，与加权信息量数值相同的一个概念。其中左边加权的量其实也就是讲右侧固定编码方式应用在别的概率数量的分布下时的期望编码数。

除了知道熵的概念之外，我们还需要了解“交叉熵”是什么
这里给出交叉熵的公式如下：

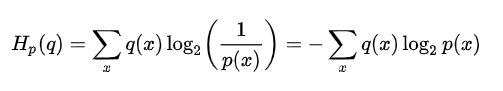
我们很明显的看到，与熵的区别就是，原先熵左右两边的分布都是一样的。因为log2p(x)就是对于一种分布中的一个出现的概率[数量比]最好的编码位，对应的左边是p(x)也就是数值上最低的样子。而在这里换成q(x)的意义就是将右边的编码方式应用到另一个概率分布下预计的输出的平均数位。也就可以量化两个分布之间的不同【与p(x)本身的熵差距越大越不同】。

既然交叉熵跟p(x)原本的熵相比就能量化两个分布之间的不同了，那不如做的再直观一点，直接相减。就得到了我们需要的KL散度,公式如下

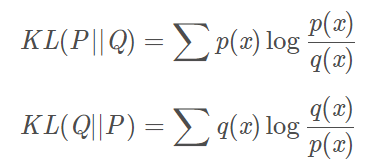
需要注意的是,KL散度的建立是在交叉熵和熵的差上的，所以要求两个分布必须有相交的地方否则无意义，而且也不对称，也非负。【这些坏毛病都是跟交叉熵来的hhhh】

JS散度

JS散度正是为了尝试解决KL散度的问题而提出的，公式如下：

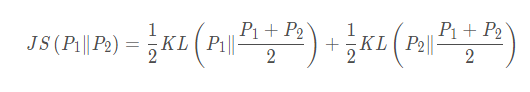
仔细看来，其中最重要的改变就是他让底变成了(P+Q)/2,解决了两个分布之间无重叠则无意义的问题，也解决了对称的问题。

不过JS散度仍然只是以KL散度角度下的解决方法，只要两个分布不相交，那么他们多近多远距离都是0。只是可以当做KL散度的改进方法来使用

F散度

F散度就是KL散度的一个泛化。公式如下：

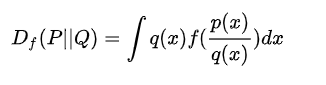
叫F散度的原因就是在f取不同函数值的时候意义不同.取-log()时就是KL散度，取别的有别的意义。

也不用探究太深，就是个这样的工具，用的时候再研究

Wasserstein距离

wasserstein距离也叫Earth-Mover距离，是最优传输理论里面的内容【听着就难好不好。。】。叫Earth-Mover距离的原因也就是这个距离的度量过程可以由搬砖过程来解释。
他可以解决没有重叠部分分布的距离度量问题，可以很自然的度量离散分布和连续分布之间的距离，而且不仅只是度量距离还会给出转移方案。

关于wasserstein距离的解释我觉得这篇csdn博客写的是最好的，若是还在的话可以直接去看那个博客。但是为了防止那个博客消失，我就在这里将他的内容以我的方式再表达一遍。中间用得到的图都是来自于这篇博客

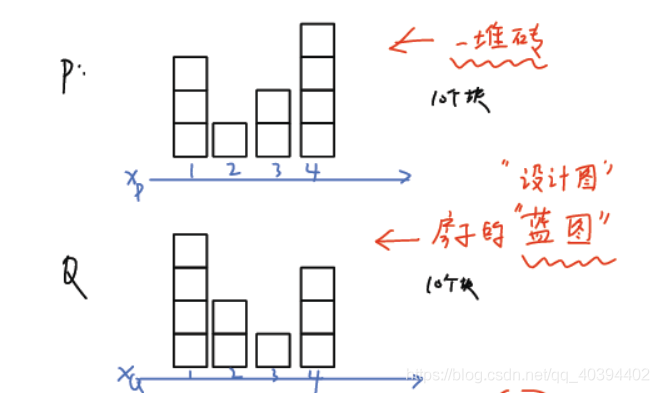
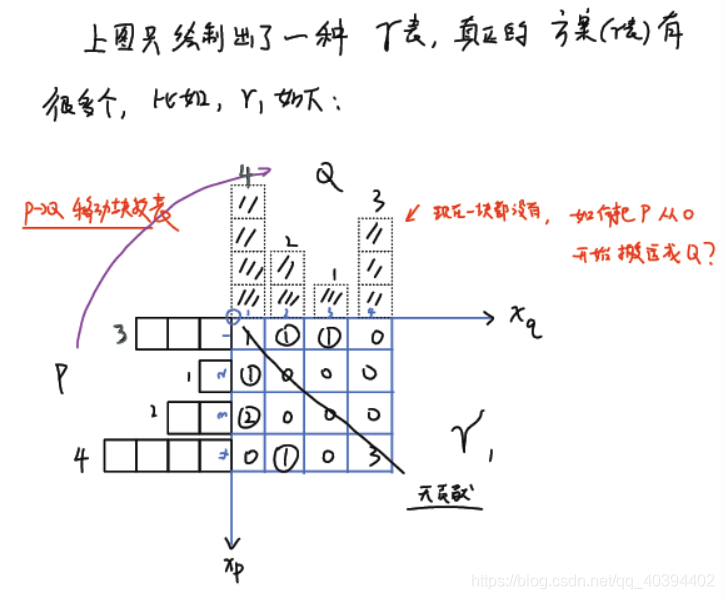
在上图中，我们要把P分布下的砖搬到Q分布的样子,方案给出的最小的花费就是wasserstein距离.这里的花费代表的是砖的重量[个数]乘以移动的距离

那这里我们给出了一个方案如下

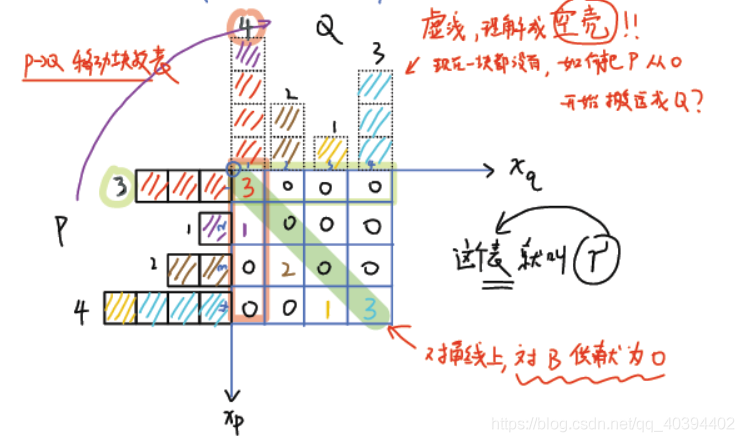
看左上角的紫箭头，这个的意思是纵坐标轴的P分布，对应位置转移多少砖到对应位置得到Q分布.对角线上的是没有实际移动的可以不用管[从1到1，从2到2，实际没有移动]

OK,我们现在将P分布的砖搬到了Q分布的样子,那我们的花费是多少？下列给出花费的计算公式。γ代表的是使用的策略，总体上就是搬了多少砖从哪儿到哪儿。

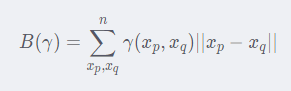
按照上述方案应用上述公式的实际的计算如下：

得到我们的花费就是4！

但是对于某一任务，不同的策略就会诞生出不同的花费，举例如下：

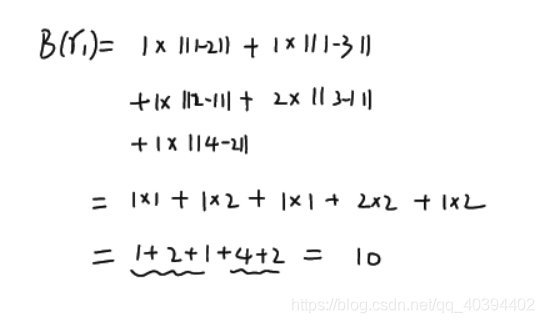
这里的花费10就比4多2.5倍

说了那么多，那wasserstein距离是什么？
先给出具体的公式

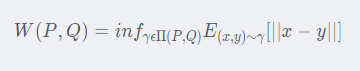
是不是看到好多公式好复杂，一下子就不想看了。。但是这里我们一起拆解一下里面的意义

↑策略符号是一个联合分布，意思是从P，Q两个所有能变换的方式[搬砖方式]里面取。
里面的E(x,y)其实也就说的是移动距离和砖的数量的乘积，构成的期望。
公式右边指的是在分配策略下的x-y构成评价标准这样

对于离散型，连续型分布是这样的

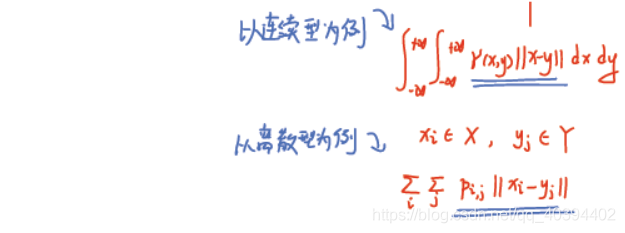
给一个离散型的实际计算的例子【用的上面那个不太聪明的例子的移动方案】

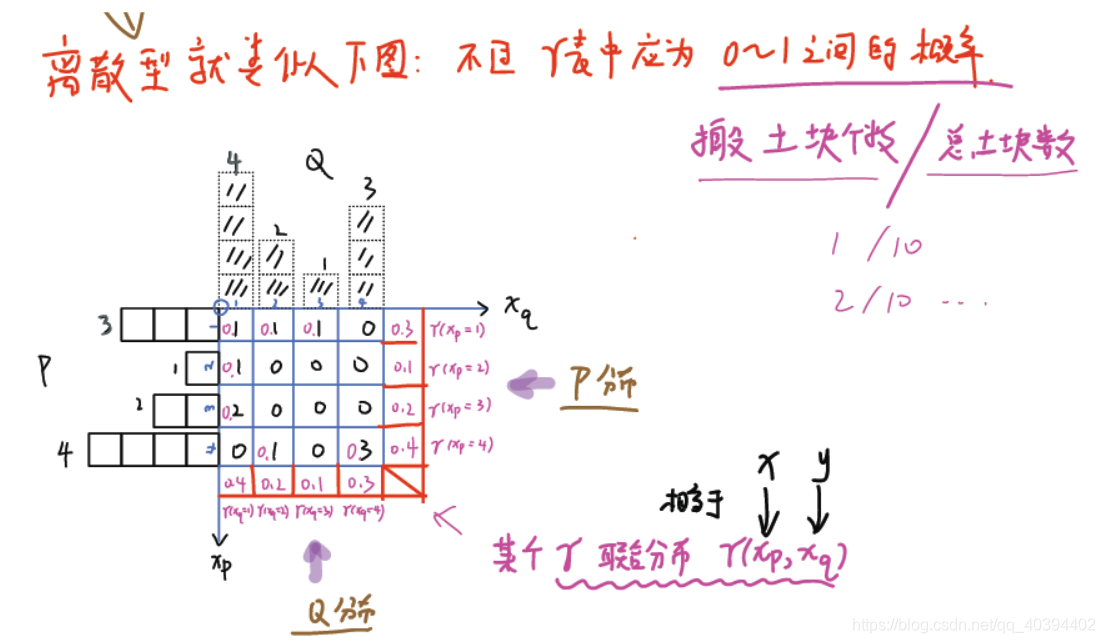
【内部都是用概率来计算的】

【若用聪明的移动方案，期望应该是0.4。但值本身没什么特殊意义】

其实关于他怎么计算连续分布和离散分布的距离的，我还不太明白。。。我觉得原文应该说的是，连续分布和连续分布，离散分布和离散分布的距离吧，处理不了离散分布和连续分布之间的距离，不然怎么都得采样或者做回归拟合。

Q.E.D.