决策树的计算思路和一个样例

还是挺重要的知识的。。

举出的样例大都来自周志华老师的机器学习西瓜书。

决策树

决策树本质上是要构建一套特征选择规则。如图例所示

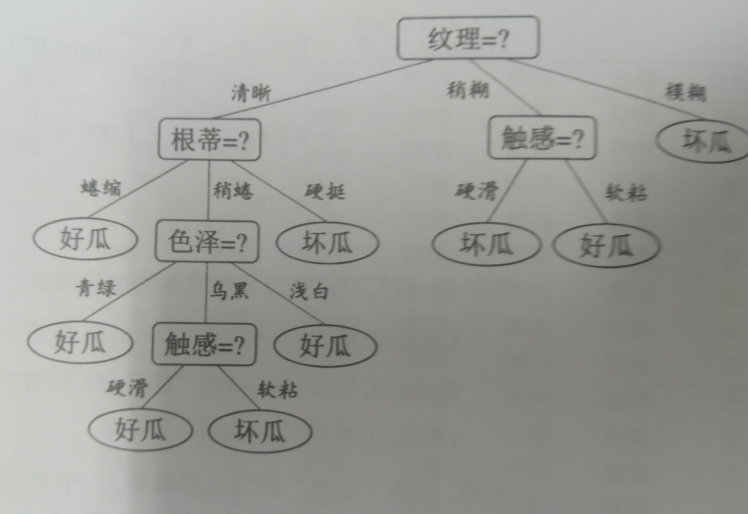
给我们一个西瓜的数据集，我们要怎么构建计算方法来判断好坏瓜这样？

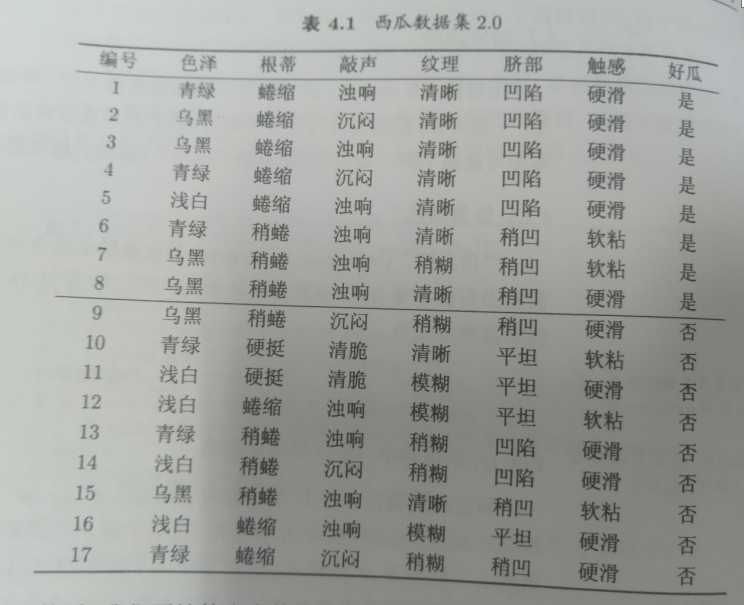
对这种结构化的数据我们有很多选择，可以编码后回归分析，可以输入到神经网络里跑，可以做knn聚类，做贝叶斯分析等。但这里我们用决策树来做，决策树对解决这种规则明确，高度结构化且分类种类较少不稀疏的分类任务有天然的优势，又快又准。

算法流程如下：

其中大都做的操作都是判断结点包含的样本是否都是同一类不需要划分，是不是所有样本只能有一种属性无法划分，是不是当前结点内部没有样本数据等。真正做的工作就是一个，第8行的选择最优划分属性。

那什么是最优划分属性？
定义上他就是最能给出影响最后Y标签的属性。所以这里需要一个合适的评价标准，什么是最能影响最后Y标签的属性？
我们朴素的考虑，最能消除某标签的不确定性的属性，就是我们想要的。这时就有了互信息量这一个天然的概念，在这里将其值引申为**“信息增益”**来处理，表示X消除的Y的不确定性的度量.

信息增益在值上就是Y的熵[本来有多少不确定性]减去对每个属性的Y标签的交叉熵[属性给出信息后Y的不确定性]，就等于属性消除的Y的不确定性有多少

计算到信息增益最大的属性就当做上面一层的分类标准，如果同层出现相同值得且都是最大的信息增益的属性则作为同层处理，最后得到我们的决策树。

给一个基于上面数据库的算法样例：

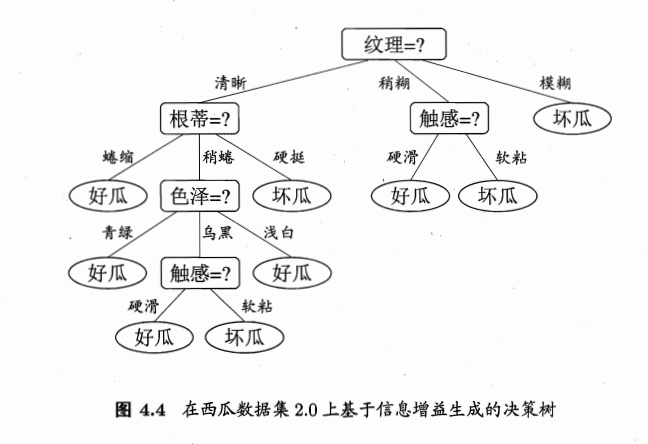
因为决策树一般也只能解决一些小规模的问题，算法性能不是很强大，所以后来又有了一种基于bagging的改进方法，名为随机森林（RF），开销小容易实现且在很多上述类似的任务中表现出强大的效果。这里不具体展开，回忆一下boosting和bagging方法就打住

boosting（提升）方法是通过根据分类器的分类结果调整单一训练数据集的权重来得到权重不同的分类器，最后将训练好的各个加权分类器线性组合到一起，都判断一下最后得到近似结果的方法
bagging（打包）方法是通过多重部分采样单一训练数据集，将每次采样得到的n个小数据集喂给n个模型进行训练，最后让那些模型依据投票法【分类问题】或者平均法【回归问题】，总之n个模型都互相平等，这样来继承学习的方法。