交叉熵为什么可以来带动学习-----知乎的末路?

似然函数推出在Φ固定下让y更

前言

这对初学者来说是一个比较经常碰到的问题了，交叉熵为什么可以作为损失函数，给梯度下降法以下降的梯度方向？他是以一个什么角度来解决的这个问题，有没有别的更好的方向来解决梯度下降的问题？这个问题弄明白了会让人感觉比较有自信比较透彻，弄不懂的话则容易自己瞎分析。所以补充这方面的知识还是重要的。

所以写了这样的一个东西记录一下学习。其实也是比较简单的

似然函数和最大似然函数是啥？

似然性是概率论中的一个概念，他跟概率有相似处但完全不同。
概率 $P(x|\phi)$ 是在已知Φ的情况下，观测到是x的可能性大小
似然性 $L(\phi|x)$ 是从观测结果x出发，预测分布函数是Φ的可能性大小

在Φ和x固定时二者数值相等，唯一的区别就是这两个参数哪个是变量哪个是已知数的区别

而最大似然估计就是在所有似然函数可能对应的Φ中选取生成x结果最可能的分布Φ的估计方法。具体给一个计算例子

由上面我们知道了似然函数一般的求法，一般是比较朴素的得知概率后求导得到在固定结果x下最大可能的Φ。为了方便求导等操作也经常使用求对数等技巧

交叉熵和各种各样的熵是啥？

我们非常常见的一个概念，熵，在严格的定义上是系统内部的混乱程度，在这里其实更多的意思是一个与他数值相同意义相反的概念——信息量。
为什么说信息量和熵数值相同意义相反？因为信息是给消除不确定性的，值越大代表能消除的不确定性越多。而熵代表的不确定性，值越大代表不确定性本身越多

这里给出熵的定义

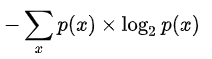
怎么理解这个式子？
右边的式子log2p(x) 其实就是自信息量【可以理解成某事件出现的概率和我们最短给他的编码位，例p(x)=1/4，log2p(x)=-2。也可以理解成单纯信息量的意义】
左边的式子 $-\sum_xp(x)$ 其实就是对每个x的最短的编码位求本身概率的归一化。负数是为了消除右边式子的负号。

更深层的理解就是右边的式子是对应每个项的信息量，左边的是那信息量有多少使用量占比。

而交叉熵(cross-entropy)就是将熵中相同分布p(x)换成不同的，见公式如下

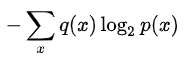
如何理解这个式子？
对同样的结果x，对用p(x)分布得到的信息量求q(x)分布的使用量占比。也就是p(x)对x的结果有了一套固定信息量的编码格式，然后对于对应的x，q(x)给了不用的x使用概率（与量占比可看成同样概念）。在q(x)使用概率下所表现出来的混乱程度

对比熵和交叉熵的式子，我们也可以遇见的，当q(x)和p(x)的分布一样或者接近时，整体值更小。

所以说，交叉熵是通过两个不同分布对对应结果出现概率的信息量的占比分配，来让自己有了评价两个分布的相似能力的。

而还有一个概念叫做相对熵，也叫KL散度

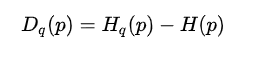
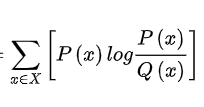
与此之外，常用的熵概念还有联合熵，相对熵。
联合熵的意思是一组概率变量的熵
条件熵是联合熵由条件概率的思想算出来的，也引出了互信息量的概念，表示在某条件下的不确定度

互信息量就是熵减去条件熵，表示原来的不确定度减去某条件下的不确定度，在值上等于在某条件下信息不确定度减少的程度。与信息增益同值，信息增益可以用来通过选择能消除最大不确定度的特征构建决策树，

KL散度是交叉熵减去熵，意义是两个不同分布的[最短编码层面数字]的距离
互信息是熵减去条件熵，意义是在一个联合分布中两个变量互相影响程度的度量【一般是X对Y】

那交叉熵与最大似然函数有啥关系？

以二元分类为例子，求某二元分类的似然函数，有
$P_{\phi}(y=1)=\phi$
和 $P_{\phi}(y=0)=1-\phi$ 。
若合并二式子，用一个式子表示的话，就得到了
$P_{\phi}(y)=\phi^{y}(1-\phi)^{1-y}$
给该式加对数，求其对数似然函数，就变成了
$L(\phi)=log{\sum^{N}_{i=1}\phi^y(1-\phi)^{(1-y)}}=\sum^{N}_{i=1}[y_ilog\phi+(1-y_i)log(1-\phi)]$
现在看看这个形式。。。这就是交叉熵损失函数！

所以从本源上来说，交叉熵也就是最大似然函数的一个马甲，求个对数就可以把二元分类的似然函数变成二元交叉熵的形式，所以也就叫交叉熵损失函数了。

之所以选取二元分类，是因为我们机器学习时最常用到的就是判断预测p是否等于y。这里取argmax之前的算交叉熵损失函数，并由其Φ的来源进行连续求导后梯度下降，来让交叉熵值更低，来让模型学习。
若使用交叉熵作为损失函数的话，模型参数更新的方向就是让交叉熵降低的方向。而交叉熵是通过让Φ和y以最短编码方向的评估，用log评估信息量是最自然最合适的方法，而评价一个系统的合理性用信息论的角度解释也是最合适，所以这个损失函数的设置还算合理。

而且有个性质是均方误差MSE没有的，那就是
若y=1时

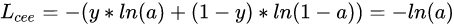
而这时

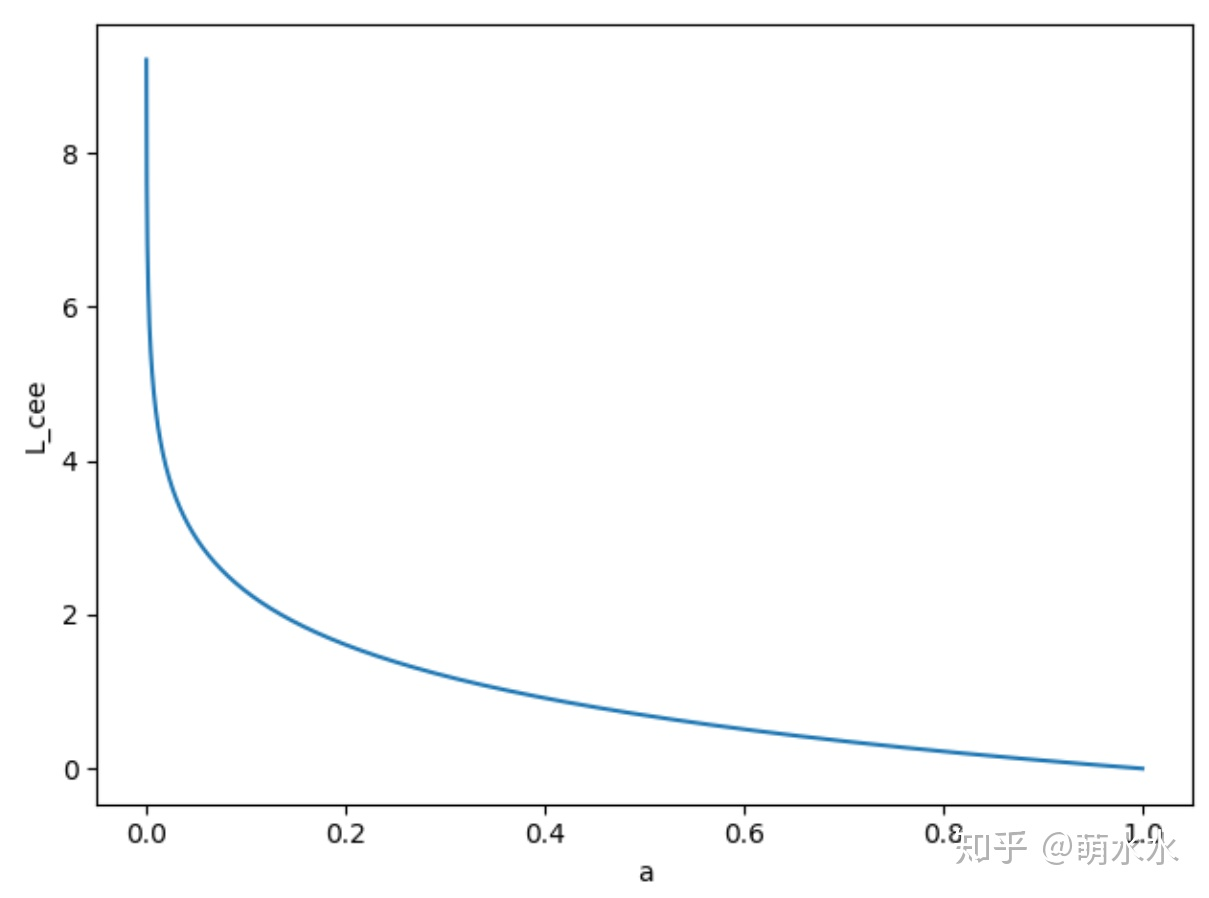
a离1越远，损失值越大，求导下降也就越快。

但是均方误差因为式子里有个sigmoid的归一化，在0,1时都没啥梯度，所以不适合解决这种问题

为什么说知乎的末路

因为在想这个交叉熵的问题的时候参考了知乎里一个最高赞的解答，那个解答是假设了一个问题，将交叉熵加了个拉格朗日算子把sum(p(x))=1的条件算进去搞了个东西，证明了交叉熵能让模型很好的学习。。当时我以为是个很好的角度，但是其中一点没有看明白，于是就去问公司大牛。。。问了问大牛后大牛一下子就看破了，假设交叉熵中y是1，a离1越远学的越快。这就证明能好好学习了。。搞着搞那就是拖了裤子放屁。实际上啥也没证明，没有证明他是以什么方式什么角度进行的评估从而让模型学习的。

然后大牛给我讲了讲知乎现在对于那些入门的，不实战的，大家基本都会的问题讨论非常多。而对那些真正实战中遇到的问题却一个回答的人也没有、、那些所谓的知乎的大牛可能更多的就是那样脱了裤子放屁这样的。所以碰上严肃问题的解决需求先看书，书中有的基本一定是对的，知乎上可以参考，可以把握新的方向，但实在不懂的也没必要懂。这跟我印象中的多看知乎其实是有出入的，给了我一个先验的高阶知识。。。所以就说这是知乎的末路，也不是以后就不看了，而是更确信的知道了知乎上的高赞不乏对知识理解不够深刻但也摆弄左右的人，之所以那么高，评论区也都在说说得好，大部分的贡献也都是别人看得懂一部分，99%那些人没完全看懂。

Q.E.D.