前言

贝叶斯定理其实就是，在统计学上对以往发生过的事情进行朴素的可信性分析。

在这儿给出定义

Y就是预测的事件
X就是目前已经知道的事件

贝叶斯定理有如下公式

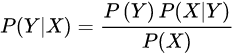
我们真实需要知道的其实就是P(X/Y),P(Y)。而这算式右边的其实都是“贝叶斯模拟出的人脑觉得的”

拿著名的童话故事狼来了当例子，故事里的小男孩因为放羊无聊，就想拿人们找些乐子。他在山坡上大喊“狼来了！狼来了！快来帮帮我啊！”

这时我们设：
A事件为小孩撒谎
B事件为小孩可信
_B事件为小孩不可信
要注意这两个事件的区别，A是小孩确实撒谎的概率,B是小孩可信的概率。这里的说法是很严格的

这时村里的大人们觉得小孩从来没有撒过谎，所以对小男孩的话非常相信P(B)=0.9。于是肯定就会放下手中的活拿着武器奔去山坡打狼。但是到了后却发现羊群好好的，小男孩在捧着肚子笑他们，说“根本就没有狼，你们被骗啦！哈哈哈”。

大人们觉得自己受到了侮辱，他们互相说，原来那个小男孩也是会不可信的，我们以后对他的话不是完全相信的了。在他们的认知中，可信的小孩撒谎的概率是P(A/B)=0.05，不可信的小孩撒谎的概率是P(A/_B)=0.8。

所以根据贝叶斯公式，大人们这次被小孩撒谎欺骗后，还相信小男孩的概率是
P(B/A) = ( P(B)*P(A/B) ) / ( P(B)*P(A/B) + P(_B)*P(A/_B) )

计算就是P(B/A) = (0.9 * 0.05) / (0.9 * 0.05 + 0.1 * 0.8) = 0.36

看来因为大人们觉得可信的孩子就基本不会撒谎，而不可信的孩子基本都会撒谎这样的观点，所以原本对孩子是0.9的相信，经过一次被骗，觉得孩子有些许不可信后，觉得孩子可信[知道了一次撒谎后，还继续相信]的概率直接成了0.36。

下一次计算时，就有P(B)=0.36，如果小男孩还是对大人们撒了谎，那大人们相信小男孩的概率就成了
P(B/A) = (0.36 * 0.05) / (0.36 * 0.05 + 0.64 * 0.8) = 0.0339

那大人可能就会彻底认为小男孩是个不诚实的孩子，以后再也不相信小男孩了

但如果第二次，小男孩没有撒谎，狼真的来了。大人们把狼打跑后，觉得小男孩虽然第一次骗了他们，但是也是会说实话的。所以大人们对孩子的看法变成了

P(B/A) = (0.36 * 0.95) / (0.36 * 0.95 + 0.64 * 0.2) = 0.7276

好消息,下次大人们对小男孩的信任度变回0.7276了，虽然比之前的0.9低了一些，但是还是比较信任的。

公式解释

这个公式有两种解释的方式，但这里只介绍一种，是P(B/A)= P(B) * (P(A/B))/ ( P(B)*P(A/B) + P(_B)*P(A/_B) )

P(B)就是原来对孩子的相信度，而后面跟着的式子是调整因素。
这种方式解释起来比较直观，调整因子就是在一定撒谎的空间里，我相信了他但是被骗了P(A/B)【因为按理论推理也是这样的，相信了他但被骗了一定是在他撒谎的空间里的，只有他撒过谎】

学到了啥

1:贝叶斯公式里面的可信度P(B)如果是1的话，那就说明他不可能出错，一切都是我的错

2:“知道你骗了人了，但是我还是相信你”是感情层面的，是不是继续相信要看感情，个人的想法等。“在你上次一定撒谎的空间里，我还相信你的概率”则是数学层面的，不带对未来的看法的。

3:贝叶斯的概率计算框架和一般的统计学不怎么一样。
贝叶斯的计算是在承认人的无知的情况下，去猜测各种的可能性这样。

4.朴素贝叶斯本质上是个生成式，而不是判别式。因为算法得到结果其实也并不需要输入个什么东西对他进行判断，而是生成各种之后的概率这样

5.贝叶斯只适合数据比较少的情景，因为再多也学不到啥了。。学习能力不够，只能那些概率到处转悠，梯度特别高这样。对训练样本的依赖性高，样本啥样他啥样

6.选不选择朴素贝叶斯，我们也要看输入的特征的数量和相关性。如果特征数量多，相关性高，那么千万别用朴素贝叶斯。。他带有很强的独立性假设，会把相关性统统忽略。但属性比较少相关性也较少时，朴素贝叶斯学习的最快效果也不差【因为天然先验的就是学这种东西的】

朴素贝叶斯做个情感分析吧

本质就是一个连乘吧。。知道了概率，然后就直接连乘一个条件概率，那tm就是一个贝叶斯了。。。

附上一个代码吧

import math
import sys
good_senten = ["high cost performance","Great place","Have a good time","quite special","good place","easy of access",
               "Very worth a visit", "tickets are cheap", "convenient traffic", "overall feels good", "worth to see",
               "very convenient traffic", "very fun", "a good place", "The ticket is cost-effective",
               "the overall feeling is good", "the place worth going", "the view is good", "the overall is not bad",
               "feel good", "the scenery is very good", "the scenery is not bad", "I like it very much", "Really good",
               "It's worth seeing", "The ticket is not expensive", "The ticket is very cheap", "The scenery is not bad",
               "The price is very good", "It's still very good", "The scenery is very good", "The environment is great",
               "The scenery is OK", "The air is very fresh", "Very worth seeing", "Very worth going", "Good view",
               "Good traffic"," Value this price", "good value for money"]

bad_senten = ["low cost performance", "I don't prefer it", "Nothing fun", "Nothing special", "Nothing good-looking",
              "Traffic is not very convenient", "Nothing special", "Tickets are too expensive", "Traffic inconvenient",
              "The overall feeling is bad", "Nothing to play", "Never come again", "Nothing to see", "Feeling bad",
              "Tickets are a bit expensive", "very bad", "The scenery is bad", "There is nothing to watch",
              "I don't like it", "The price is a bit expensive", "cost performance is too low", "I feel not good",
              "not high cost performance", "Not very fun", "Tickets are not cheap ", "traffic is not convenient",
              "the scenery is not good", "nothing to play", "too commercial", "tickets are expensive",
              "fare is a bit expensive", "nothing to see", "price not cheap", "price is very high", "ticket too expensive",
              "The traffic is not good", "The ticket is too expensive", "The scenery is very poor", "Not worth the price",
              "The traffic is bad"]
ngood=0
nbad=0
good_words={}
bad_words={}
for word in good_senten:
    for s in word.strip().split(" "):
        ngood+=1
        if s not in good_words:
            good_words[s]=0
        good_words[s]+=1

for word in bad_senten:
    for s in word.strip().split(" "):
        nbad+=1
        if s not in bad_words:
            bad_words[s]=0
        bad_words[s]+=1

p_good=1
p_bad=1
list = ["high cost performance"]
for s in list[0].split(" "):
    if s in good_words:
        p_good*=(good_words[s]/ngood)
    else:
        p_good*=1/ngood
    if s in bad_words:
        p_bad*=(bad_words[s]/nbad)
    else:
        p_bad*=1/nbad

if p_good>p_bad:
    print(1)
else:
    print(0)

上面是个easystart，我们单独提取出来贝叶斯概率计算的那部分来看看

p_good=1
p_bad=1
list = ["high cost performance"]
for s in list[0].split(" "):
    if s in good_words:
        p_good*=(good_words[s]/ngood)
    else:
        p_good*=1/ngood
    if s in bad_words:
        p_bad*=(bad_words[s]/nbad)
    else:
        p_bad*=1/nbad

if p_good>p_bad:
    print(1)
else:
    print(0)

这部分就是贝叶斯概率计算的部分。。首先把概率初始化成1，然后如果在好or坏的里面存在or不存在的话，就直接连乘一个条件概率【在所有带标签的样本空间里，拿到这个的概率】好坏都连乘，连乘到最后就ok了。。

可能有些小伙伴会觉得p_good*=good_words[s]/ngood这个连乘跟我们上面的P(B/A) = (P(B)*P(A/B))/(P(B)*P(A/B) + P(_B)*P(A/_B))根本八竿子搭不到边啊。。但是我们仔细想想，这个P(B/A)不就是下一次是P(B)嘛，而分母上的不就是P(A)嘛，也就是所有该样本的空间概率，乘以分子上的在这个样本里面的频率当做概率。

与放羊娃儿的区别在于放羊娃有一个“可信or不可信的孩子撒谎的概率”，我们要连乘也就是要算成撒谎的概率，两个撒谎的概率成可信的概率。本质上还是一样的。可信的孩子和不可信的孩子也只不过是选择，选择后还是要算造成的后果的概率，就多了这么一步罢了

总结一下情感分析的过程：

洗数据，做词表做统计，拿到输入分词，给p_good和p_bad连乘在所有词表中当前词的概率分布，如果没有就看作1这样。

最后乘出来就有分类结果了，其实从直觉上也好解释，没有就连乘1/ngood，有就连乘频率/ngood，这样就能扩大概率。但是ngood和nbad不一样，所以还是存在悬念的

但是单纯做贝叶斯在性能上会有压力，主要有几个大问题：
1:贝叶斯独立性假设，忽略上下文信息
2:单纯词频信息不考虑重要性
这时候第一个想到的是TF-IDF和n-gram来完善算法

TF-IDF那就是词频*上下文出现的次数比例，算边缘概率时挑到了词，对那个词算边缘概率输入到贝叶斯公式里算就行

n-gram是把整个都变了，输入的是词组的统计，输出的是词组的统计概率。

这样能解决重要性，和上下文信息这两个问题

插入一个knn的

knn就是k邻近算法，带有聚类性质的，给原来带有标签的数据构成向量化后进行聚类性质的多数投票重分标签的算法

比较适合label比较多样本向量聚类又比较明显的应用场景。比如说基因这样的。

对k值太敏感，而且可解释性没那么强

可以尝试一下只训练，重新分配标签加强聚类性来洗数据

Q.E.D.