排雷排雷。。。之前经验分享会上的LDA算法指的是潜在狄利克雷分配(Latent Dirichlet allocation)。而不是线性判别分析的那个LDA（Linear discriminant analysis）
前者是文本集合的生成概率模型，后面是线性判别找主题内方差最小主题外方差最大这样一个加权的算法。
总之先写个PCA
PCA主成分分析算法
概念解释
先解释些基本概念，方差、协方差、和协方差矩阵。
方差和协方差都是在统计学上对数据的描述。
方差是度量单个单个随机变量内部数据的离散程度。
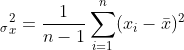
右边的x是平均值，n是一共多少数据
协方差则是描述两个随机变量之间相似程度的工具。
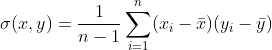
而方差也正是方差概念的扩展，是随机变量(参数)自身的协方差，自己的数据与自己的数据的相似程度
而协方差矩阵则是
包含矩阵各个位置元素对应的协方差的矩阵。对角线上可以看作是方差而已。
经常会有除以协方差矩阵的操作，这是为了消除大方差带来的影响。所以求协方差这件事经常会有的。而矩阵自身的协方差矩阵也会叫协方差矩阵，而不叫方差矩阵。
算法思想和流程
PCA主成分分析也就是想找到最能代表数据的维度表示，来对数据进行降维操作。
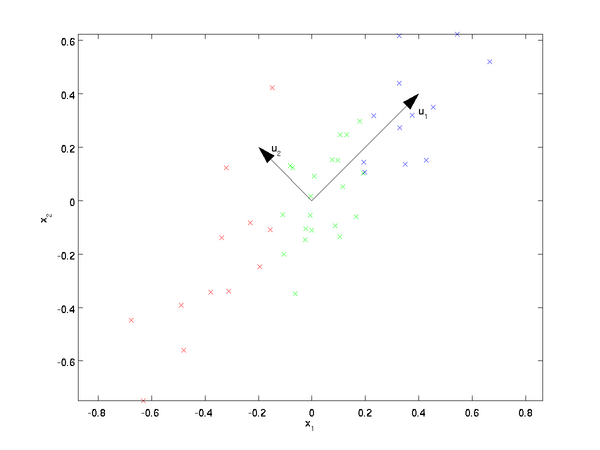
观察上图，如果要对该数据进行降维，按照u1和u2哪个维度更好？显然是u1更好，因为在u1的轴上数据尽可能的均衡分散。那我们怎么来找到这个u1轴，并将数据都投影到u1的轴上？
我们来重新回顾一下方差的定义。方差就是描述数据分散程度的指标。这正好就跟我们PCA的要求吻合。所以我们的任务就成了在该表中找到一个让所有数据方差最大的方向轴。
所以我们直接对原来的矩求一个协方差矩，对协方差矩进行一个EVD特征值分解(SVD也行)，选取其中前k个(k是要降维到的维度数)最大的特征值和其特征向量W。也就是得到了协方差矩阵所有维度里，最能代表方差最大的那几个特征值和特征向量。
因为特征分解的目的，就是找到矩阵隐含的只有缩放特性的方向和他们缩放的比例。而其中缩放比例更大的方向也就代表了影响最大的方向（线性变换角度），就等于找出了协方差矩阵里面所有协方差加起来最大的k个方向(矩阵数值角度)【完全把协方差矩阵分解了，在缩放比例更大的方向中混入缩放比例更小的方向的投影都是对整体值的缩小。】。
上面这段看不懂的可以看看下面对特征值和特征向量的深度思考的总结。看明白了就不用了
既然得到了协方差矩阵里面协方差加起来最大的角度方向，那就代表该角度上数据的方差最大最分散。直接把原来的数据乘以该角度投影到该角度上。因为W的维度比较小,所以也就降维了。这就是PCA的算法思想。
PCA的流程就是：
- 先对数据进行“中心化”。
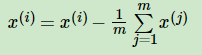。增大鲁棒性，放大方差效果 - 求出矩阵协方差矩
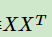
- 对协方差矩进行EVD或者SVD后取出最大的k个特征值对应的特征向量，标准化后组成W矩阵。
- 对原来的每一个数据进行按照该方向映射。
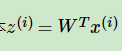
- 得到了PCA处理后的样本特征集
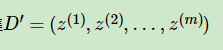
PCA数字计算实例
落实到直观的数学计算上才能算是一个好的理解。。
PCA的优点和缺点吧
优点：
1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。
2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。
3）计算方法简单，主要运算是特征值分解，易于实现。
缺点：
1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。
对特征值和特征向量的深度思考
问题：特征值和特征向量的意义是什么，凭什么算到特征值和特征向量的组合，就能说那个是最大的轴？原理是什么。不旋转不投影的纯粹缩放这我们知道，但是为什么这个就是不旋转？随便一个正交矩加上那个对角化的矩阵都行？
因为特征值的组唯一啊，这里存在一个假设，是矩阵可以求出k个特征值和特征向量。。特征分解的公式就是提供了强行要求得到的特征矩阵的形式（对角矩），只要那个是对角矩，另外一个就肯定被分解成不旋转的特征向量方向（对角矩就是把只有缩放的元素分解出来了，剩下的肯定都是方向）
我们得到了变化最大的方向(把矩阵看成线性变换来看)，自然也就能知道哪里的值大，哪里更主要。
这里做个总结。在把矩阵看成线性变换的角度，特征分解EVD的目的就是在尝试在可以被特征分解的矩阵上，找出变化最大最小排序的方向和其缩放的数值。要与被分解的矩阵乘的矩阵，与特征向量方向共轭的就只受到缩放的效果了，不共轭的会会收到所有特征向量和特征值的拉伸
而在把矩阵看成值得角度来看，EVD的目的是尝试找出某角度有没有各元素加和的最大最小值排序方向。最大最小值排序用特征值来判断，在这里特征值应该没有什么更加具体的实在意义
想要找最大变化方向可以SVD可以EVD，二者实在效果差不多。只不过SVD任何矩阵都能做，EVD要求实方阵，也就没有了SVD的投影分解这一功能。旋转和缩放还都有，但是特征矩特别的还可以为负数。就这些了吧
协方差矩阵：
两种LDA（待补充）
Q.E.D.
Comments | 0 条评论