矩阵分解方法(更新到QR，LU，LR)

矩阵分解方法是一种虽然基础但是可塑性和直觉性都非常强的方法，这种方法往往能给信息冗杂的矩阵以简化和信息融合，让我们更好的认识矩阵和他隐藏的信息。
他在广义上也可以算是一种知识表示学习，但也可以作为直接的解码来使用。我感觉是一个非常好的工具，所以在这里记录学习。

预先假设读者掌握基本的线代知识（什么是基础呢...非常常见的名词能粗浅的知道什么意思就好吧）

EVD特征值分解(方阵，特征值可以为负)

因为比较基础，所以这里只提供一个例子

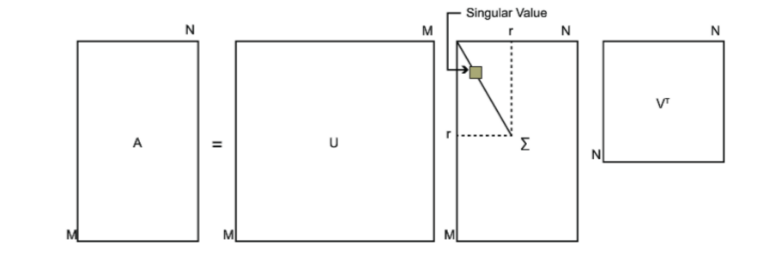
SVD奇异值分解(基本任意矩阵)

一个线性变换由旋转，缩放，投影三个共同作用而work。我们在对一个矩阵进行线性变换时(与某矩阵乘)，要乘的矩阵发挥的作用不外乎这三种。而SVD天然就是把矩阵的这三个作用分解出来的算法。

SVD经常会被跟特征值分解来做比较，因为二者都是给一个矩阵(线性变换)找一个特殊的基，来以另一个角度来看待矩阵(线性变换)。特征值分解的公式是AX=XΛ 和其变形 A=XΛX^(−1)，与下列SVD的方程确实很像，但是二者发挥了很不一样的作用。

对矩阵A进行SVD的公式为：
A=UΣVT

EVD对矩阵的分解可以看作是会将另一个矩阵从x基的空间，经过Λ的缩放后又旋转回来x基的空间，这其实就是没有旋转了。。因为中间没有基的改变。所以EVD就是找一个特殊x角度的基，让旋转没啥用而更好的表示。

但SVD中我们又怎么得到U和V?这里采用验证的方法，提前告诉你A^{(T) * A的特征向量是U,A*A}(T)的特征向量是V,然后来验证。

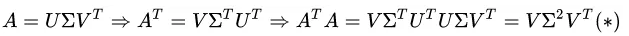
其中上式隐含了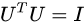和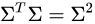。这是为什么?
因为U，V得到的途径的本质，是对A与其转置的乘积得到的方阵进行EVD而得到的特征向量。而特征向量

FunkSVD

QR分解(必须满秩且不唯一，特征值特化)

QR分解可以看作是三种实现途径：
1：施密特(Schmidt)正交规范化
2：吉文斯(Givens)变换
3：豪斯霍尔德(Householder)变换

QR分解其实就是把矩阵分解成一个正交矩阵一个上三角矩阵。还算经常的用来求特征值，因为他比较直接了当的算出来了特征值【缩放比例】，而且没有求多余的那些旋转的方向什么的【因为包含特征值的矩阵是上三角，所以说那边的矩阵虽然是正交矩，但是并不代表矩阵分解出来的所有的旋转】。

既然要把一个满秩的矩阵来分解成一个正交矩阵和一个上三角矩阵，那已知那个满秩的矩阵，再将其形式变成一个正交矩或者上三角矩中的任何一个，那另一个未知的矩就自动算出来了。下面的schmidt就是强行凑正交矩，givens就是强行凑上三角矩阵，householder我还没太看懂就先搁置一下。

schmidt正交规范化

如前面所说，schmidt正交规范化就是给原来要被分解的可逆矩阵【满秩】做一个基于形成上三角中间处理式的强行正交化。求出正交的矩阵，知道待分解矩阵，自然就能知道剩下的上三角的带有特征值的矩阵。

上面标准正交向量组的式子中间是求出来后单位化的提醒，这个先不用管，就看最右边和最左边的等式。
a是任意可逆矩里面的向量,这里我们要做的就是要逐渐构建一个新的正交向量组。所以就用逐渐加a乘与其相匹配的任意向量组T等于的方式来完成正交向量组的构建。【因为A可逆满秩,所以多加任何一个at都可以有一个新的正交向量被构建】

那为什么不用t11a1,t22a2,t33a3来构建正交向量组里面每个向量？因为这样不能确保构建出来的向量真的互相正交，除非a的方向本身就互相正交。

我们根据这一套构建出了新的正交向量组

在其中我们要强行要求正交向量组保持正交的话，就有如下的条件

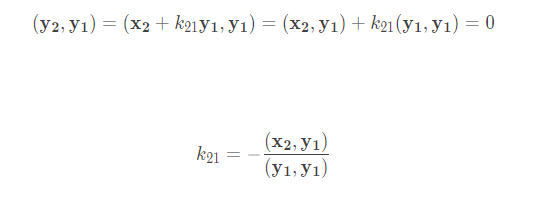
其中y1,y2就是正交向量组里面的向量，x就是a，k就是t。(y2,y1)就是y2与y1的乘积，下面的(x2,y1)也是x2与y1的乘积这样。
其中y1=x1,y2=x2+k21y1,k21=(x2,y1)/(y1,y1)。这样一步步就把y和k都算出来了。不涉及什么旋转，这就是在组合等式的角度硬凑。

而R=T^ -1，得到A=QR，对T求个逆得到R就完成了矩阵的分解了(因为上三角矩阵的逆依旧是上三角矩阵)

按照管理来个计算的例子

givens变换

对这个好像有挺多不一样的理解，但是我认为比较好的理解就是任何一个满秩的矩阵都可以达成一种上三角的矩阵形式。而达到这个形式本质上就是要通过矩阵旋转来完成。所以说在这里我们直接一个一个的给他炫咯。。
而恰好旋转矩阵他肯定又是正交矩阵，所以说正好构成QR分解的条件之一。我们组建旋转矩阵，把可逆矩阵旋转到上三角的形态，就完事了
先来看看比较简单的二维情况：

givens算法就是乘以一次G就等于选定一个位置给炫成0，其他位置的元素受到影响。只要满足

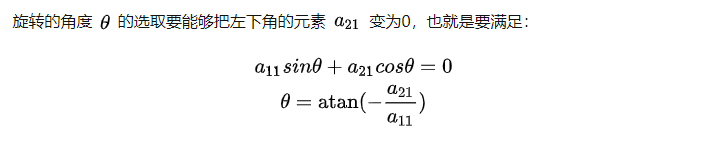
就可以。而a11,a21我们都是知道的，所以也能求出来。这样A就慢慢变成上三角了

再到更复杂的情况下就是

这里有一个固定的模式，就是从左到右每列按顺序换，每一列内从下到上按顺序换。
需要注意的是，取旋转矩阵的三角位置的原因是旋转要对指定维度的元素进行旋转，当sin,cos集中在2,3维度上那就是要对2，3维度旋转。集中在1,2维度就是要对1，2维度进行旋转从而对元素造成影响。而且受影响的往往还是与其sin,cos相对应的那个位置的元素。

算出来G矩阵后，由于GA=R给他来个求逆，也就算出来A=QR了。【R是上三角】

按照惯例来个计算实例结束：

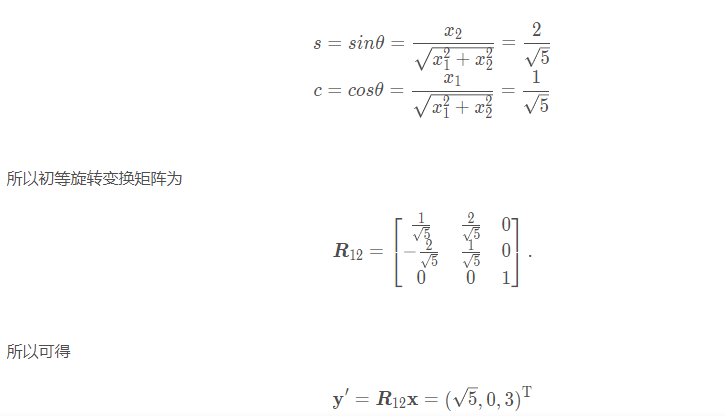
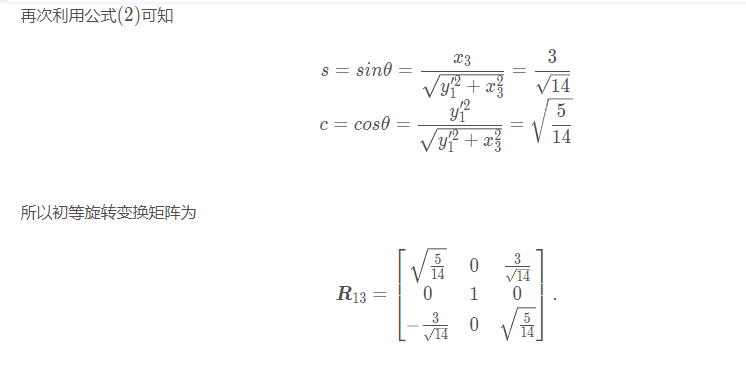
y就是旋转过的了
最后求解出

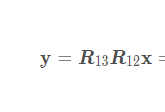
再求R的逆,移动到左边那整理好的上三角。就是标准的QR分解

每种方法的适用场景

实际情况下要求特征值的情况也不少，我们会经常在各种场景下用到QR分解。但是三种常用方法都有什么优点和缺点？
1：schmidt根据等式求k
肉眼可见的计算量大需要保存的东西多，对内存和算力的要求直接指数增长。所以比较适合小矩阵。因为实际上的矩阵0按照这个方法也都需要算，所以不适合稀疏矩阵。但正交基逐步生成，所以算法可以随时停，只要留着正交基就能很快的继续。
2：givens炫他就完了
因为是0就自动不用炫了，所以最适合稀疏矩阵，而且旋转给原矩阵带来的影响很小不会做无效操作，可以说是特别适合了。。但缺点是一旦到大稠密计算，优势就基本没了或者说反而成了负担。施密特人家还是由k值一算一个维度一个基【虽然k很多所以也半斤八两】，这个到极限大稠密矩阵要比施密特都不适应。

3：Household

不显式计算Q正交矩阵,所以中间省去大量的计算.最适合稠密矩阵的QR分解。但是对稀疏矩阵会产生大量的无效计算。
【因为暂时没看懂所以先这样】

LU三角分解(只要求n阶方阵，不一定存在)

LU三角分解就是给原矩阵分解成上三角和下三角的矩阵解析。条件当然是方阵且可逆【高斯消元就不用可逆，比较宽泛】。在矩阵右边做一个方阵的单位矩阵增广，用于记录左边的变化。对左边的原矩阵做一个上三角的构建，因为右边是单位矩阵所以自然而然就成了下三角矩阵，也就成了LU(low and up)分解
LU分解对原理不需要解析太多，重点是过程和意义的理解。
我们对A进行LU分解，的意义就是调整矩阵A的可计算性,让其更容易解Ax=b的问题。对于一个超大矩阵求解Ax=b的问题，若是A不怎么变、x和b一直变的话，那一直用高斯消元8行，计算量太大。而先用LU分解给矩阵分解了，到时候计算只需要计算上三角下三角就行了，且这是对A的永久改变，以后遇到更多场景LU分解也就做一次。【虽然单次来讲，对一个超大矩阵，LU分解比高斯消元要麻烦】

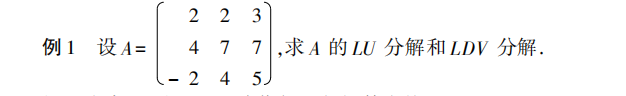
具体怎么接Ax=b的问题？

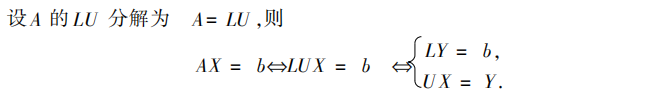
根据以上的理解，得到式子

LR满秩分解(不唯一但总存在)

说是满秩分解，但是并不是只有满秩矩阵才能做的分解，任何非零矩阵 A ∈F m × n，都存在满秩分解。这里满秩分解的意思其实是分解成两个行列分别满秩的矩阵。
LR满秩分解虽然不唯一，但是总是存在。只要是非零矩阵。

其实LR满秩分解的motivation跟LU分解有相似之处，也是在右边做一个单位矩阵的增广，然后尽可能做成阶梯式。(A|E) = (C|P)。这时P*A = C。这个就是记录的性质吧..然后怎么LR分解呢？我们从变成的阶梯式的C中取行方向的满秩的矩阵(尽管他可能不满秩)，再根据C的秩从P的逆中取相应的列方向的符合C的秩的矩阵[会丢下些值,但没关系.他们本来就对投影和秩没啥影响，只是可能对缩放和旋转有影响]

接下来以一个例子做说明：

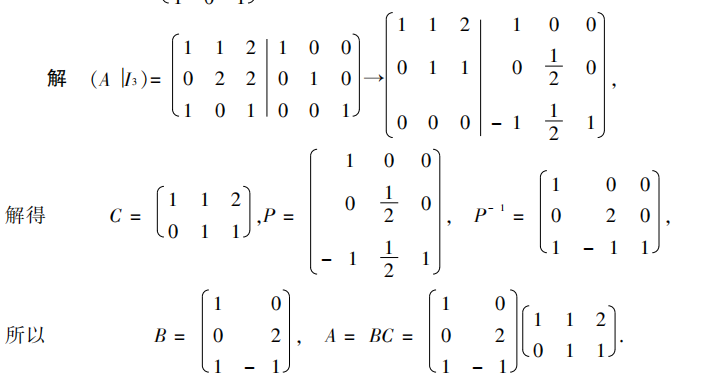
这就是行增广方向的LR分解。还有个列方向的但是知道就行

还有一种解的方式要更简单直观。经过初等变换的行列维度只要是证明是线性无关的，那就一定组成秩。如果我们将矩阵变成了hermite标准形也就是最简式，那通过观察(1,0,0),(0,1,0),(0,0,1)的位置就能直接从原矩阵中取出对应位置的列满秩矩阵B，C就是hermite最简式的非零行，从而完成满秩分解A=BC.

谱分解（求矩阵幂，要求正定阵（默认对称））

主要是为了求矩阵幂，连乘那种。目前不太懂应该怎么用

A互异的特征值集合｛λ１， λ２，…，λs｝称为矩阵 A 的谱，矩阵的谱分解是讨论矩阵可相似于对角形时，依 A 的谱或特征值把矩阵 A 分解为矩阵和的形式的一种分解．从分解中我们可得到矩阵可相似于对角矩阵的又一个充分必要条件．

极分解(方阵，若A可逆则唯一)

极分解是针对复数矩阵的。。。现在用的少些先不学了

cholesky分解

就是LU三角分解在正定矩时的特殊情况。分解成一个下三角矩阵和他的转置【那不就是上三角恋嘛。一样的计算。

单边雅可比方法并行计算SVD(没看懂)

学的时候复习补充的知识吧

高斯消元。。

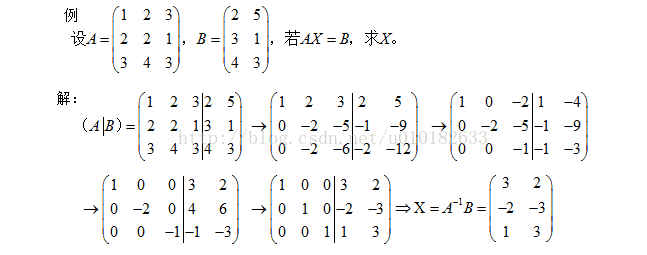
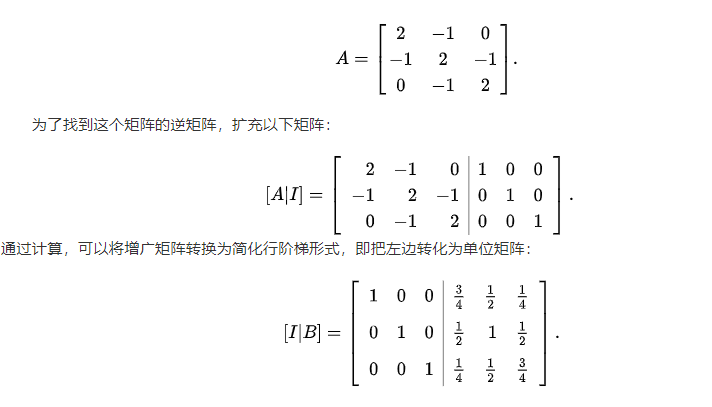
学习矩阵分解方式时对矩阵的更新理解

正交矩阵由相互正交的向量组成，本身只有旋转的特性而没有缩放和投影
那个经典B = MAMT的可以理解成对B的一种分解，如果A是行列式而M正交的话
特征值当然不是随时都有，如果有，那就是表示矩阵原始组成方向。可以理解成一种原子性
上下海森堡矩阵就是...你懂的
可逆就是满秩。正交矩阵一定满秩。
相似也就是那个特征值一样的那个意思
矩阵的逆在空间中也是“变换回去”的意义，在数值上也是“矩阵除”的意义
任意矩阵A与A的逆矩阵相乘等于E，只是正交矩的转置等于其逆矩阵，因为正交矩只有旋转的特性
行列式是线性变换对面积改变的比例。所以行列式为0的时候，等于不满秩。行列式对特征值有指导意义。而行列式为负数时表示发生了取向反转。这个性质跟分解后的特征值一样。实际上，特征值的乘积就是行列式的值【特征值的和是矩阵迹的值】
矩阵的逆的直观看法是，把投影、旋转、缩放到倒过来算。而矩阵的转置就是把旋转倒过来【没错，只是把原来的倒过来算，】。正交矩阵又只有旋转，所以正交矩阵的转置等于其逆矩阵。

矩阵等价相似合同

矩阵等价：对同型矩阵A、B，存在可逆阵P和Q，使得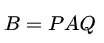。充要条件是A和B的秩相等
矩阵合同：对同型方阵A、B，存在可逆阵P使得
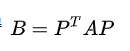
矩阵相似：对同型方阵A、B，存在可逆阵P，使得

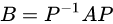
就严苛的程度从宽松到严格来说，等价(只要秩相同就能互相转换)->合同(秩和正负惯性指数相同)->相似(秩，正负惯性指数，特征值均相同)

1：正惯性指数相同的等价矩阵是合同矩阵
2：相似矩阵未必合同，但正交相似矩阵必为合同矩阵，正交合同矩阵也必为相似矩阵
3：如果A与B都是n阶实对称矩阵，且有相同的特征根．则A与B既相似又合同
4：相似矩阵必为等价矩阵，但等价矩阵未必为相似矩阵
5：因为矩阵合同的概念基本只用在二次型，而二次型用的矩阵天然是实对称矩阵。两个实对称矩阵合同的充要条件是它们的正负惯性指数相同，如果再正交的话那就是又相似又合同